傅里叶变换原理(简易)
傅里叶变换
连续与离散
一般人们口中所说的傅里叶变换都是指连续傅里叶变换,针对的是连续时域信号。维基百科上是这么描述连续信号的:
连续信号或称连续时间信号是指定义在实数域的信号,自变量(一般是时间)的取值连续。若信号的幅值和自变量均连续,则称为模拟信号。根据实数的性质,时间参数的连续性意味着信号的值在时间的任意点均有定义。
简单来说,对于一个sin函数的连续信号,其波形长这样:
对于计算设备的信号处理,因为采样设备的采样率是有限的。因此得到的采样信号都是离散的,所以就有了针对离散信号的离散傅里叶变换。维基百科是这么描述离散信号:
离散信号是在连续信号上采样得到的信号。与连续信号的自变量是连续的不同,离散信号是一个串行,即其自变量是“离散”的。这个串行的每一个值都可以被看作是连续信号的一个采样。由于离散信号只是采样的串行,并不能从中获得采样率,因此采样率必须另外存储。以时间为自变量的离散信号为离散时间信号。
离散信号并不等同于数字信号。数字信号不仅是离散的,而且是经过量化的。即,不仅其自变量是离散的,其值也是离散的。因此离散信号的精度可以是无限的,而数字信号的精度是有限的。而有着无限精度,亦即在值上连续的离散信号又叫抽样信号。所以离散信号包括了数字信号和抽样信号。
傅里叶变换公式实际意义
直接看傅里叶变换公式:
$$
\begin{align}
{F}(\omega) = \int_{-\infty}^{\infty} f(t)e^{-j\omega t}dt
\end{align}
$$
其中
- $f(t)$频谱未知信号,我们就是对这个信号做傅里叶变换。
- $F(\omega)$为傅里叶变换后的频谱函数。其自变量为$\omega$频率。
- $e^{-j\omega t}$为复信号
要理解这个公式,关键就在于$e^{-j\omega t}$怎么理解。本科学过复变函数的同学应该都知道,指数复变函数是可以转化为三角函数形式的。其变换公式如下:
$$
\begin{align}
e^{-j\omega t} = cos(\omega t)-jsin(\omega t)
\end{align}
$$
$$
\begin{align}
{F}(\omega) = \int_{-\infty}^{\infty} f(t)(cos(\omega t)-jsin(\omega t))dt
\end{align}
$$
由上式可得,要想得到信号频域与相位信息只需要将信号与复数信号做乘法后积分。
信号的筛选
简单概括公式所表达的实际意义后,我们再来看为什么要这么做。废话少说直接按照傅里叶变换公式所描述的做法,将信号与各已频率信号乘法后积分,写一段简单的matlab程序。最终结果如下图:
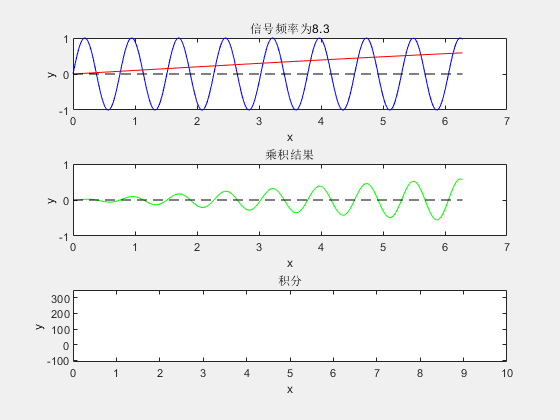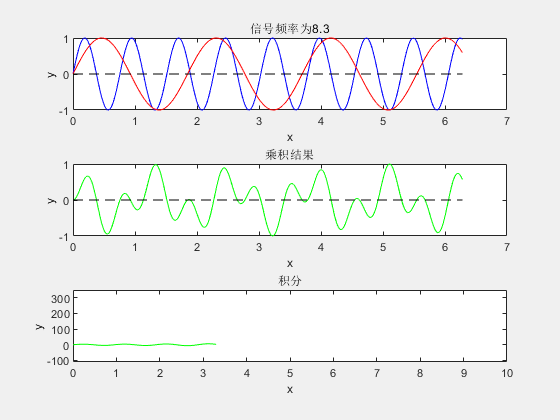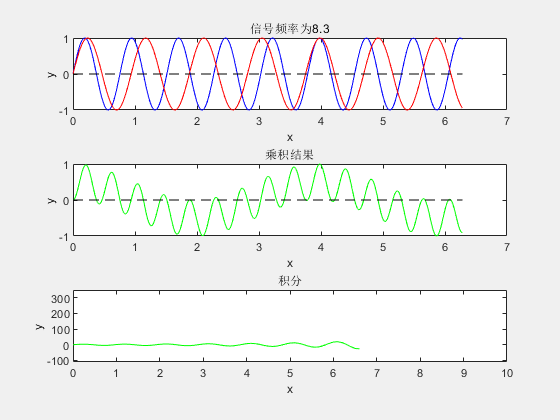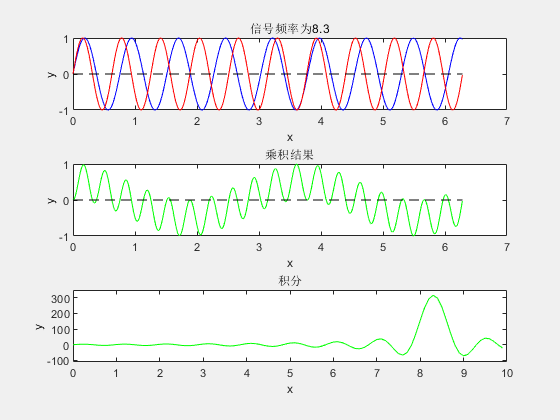
- 框图1内蓝色信号线为MATLAB生成需要做傅里叶变换的随机频率的信号(未知信号),红色信号线为频率不断增大的正弦信号,红色信号是人为生成的(基信号),因此其频率是可知的。
- 框图2为两正弦波相乘结果。
- 框图3是对正弦波乘积结果的积分。
从图上可以很清楚直观的看出,当未知信号与基信号频率相同时,他们乘积的积分达到了最大。而这个积分最终的图像是不是就很像信号经过傅里叶变换后的频域图像呢!利用了乘法负负得正的特性,当基信号与未知信号频率完全相同的时候,其时域上乘积全为正数。因此,此时的积分达到最大值。通过此类操作即可得到未知信号的频率。
说人话,就是用各种频率的基信号与未知信号做对比,看看哪个频率的基信号与未知信号最像!!!,而这个对比的方法,用数学来描述就是先相乘后积分,这样描述的话,是不是听起来就没那么复杂了。
用公式描述就是:
$$
\begin{align}
{F}(\omega) = \int_{-\infty}^{\infty}f(t)sin(\omega t)dt
\end{align}
$$
可以看到,已经离上文所示的傅里叶变换公式(3)有点相像了!
Q: 单个频率成分信号可以,那多个呢?
那自然也是这么做的,废话少说,直接上图:
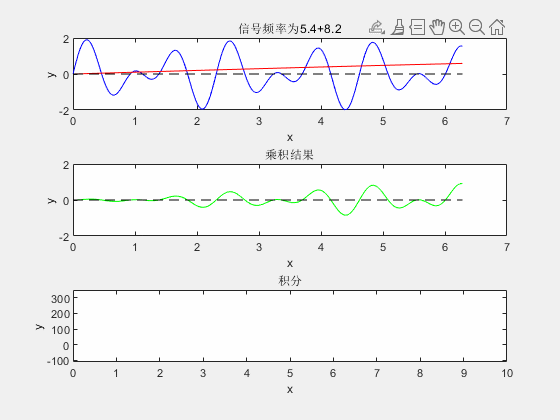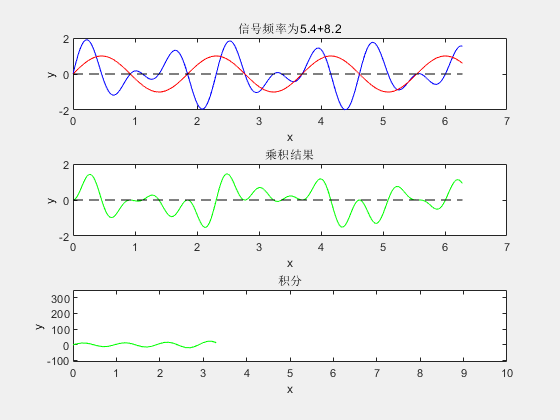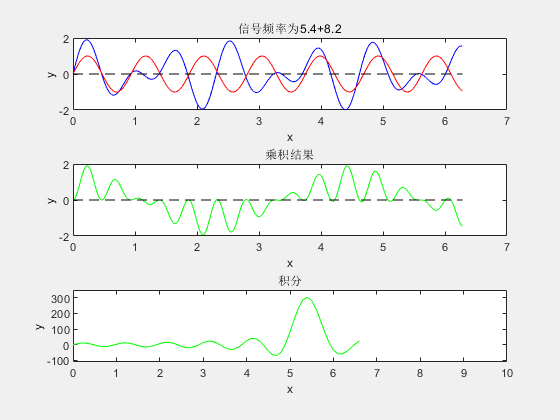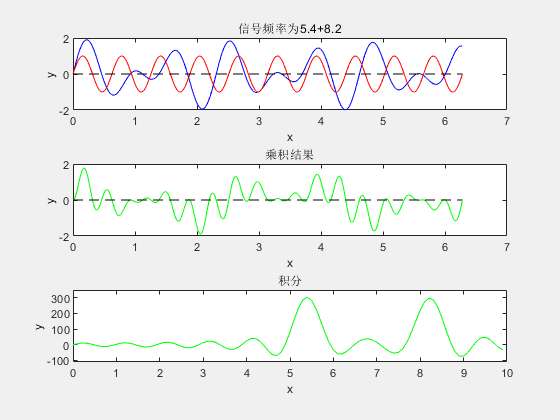
由此可以看出,用这种方式可以筛选出未知信号中各种频率成分,至于为什么可以?前面说过了,本文只讨论傅里叶变换做法,暂不对其数学原理做深入探究,想要深入了解的朋友可以自行搜索,或关注我的博客,或许不久后将更新此方面的内容。
初始相位的问题
上文所讨论的对未知信号频率的筛选,全部都是建立在未知信号相位为0的情况下。但是实际使用过程中,信号的相位与频率都是未知的,若只使用上文(4)所描述的方式肯定是不行的,如下图:
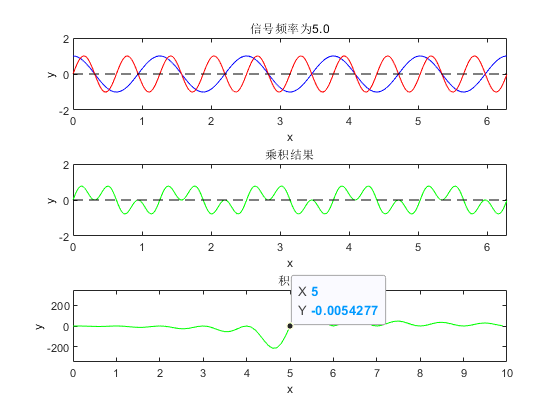
可以看到若未知信号的初始相位为90°,若还使用公式4,得出的结果与实际就有误了。
此时再回头看看傅里叶变换的公式,不难发现,傅里叶变换使用的是复数信号。$e^{-j\omega t} = cos(\omega t)-jsin(\omega t)$。也就是说傅里叶变换对未知信号使用复数信号相乘后求积分。而不是只对单个正弦信号做比较。
不难看出,傅里叶变换的结果是复数信号,其结果实部的值就是表示未知信号与cos信号的相关度,虚部值表示未知信号与sin信号的相关度。由此可以看出,傅里叶变换的结果还包含了未知信号的相位信息。
为了分析其频率信息,我们可以对结果做取模开方处理,也就是:
$$
\sqrt(R^2+I^2)
$$
结果如下图:

可以看到位置信号的频率成分已经被解析出来了,这里注意一点,上文是做了开平方处理,也就是说解除了在正频域,在负频域也有频率分量。
离散傅里叶变换(DFT)
离散傅里叶变换实际上是按照傅里叶变换的定义对离散的数字信号进行计算,积分变成了连加,频率间隔根据采样点数的倒数确定,公式如下:
$$
X[k]=\sum_{n=0}^{N-1}{x[n]e^{-j(2\pi/N)kn}}
$$
采样带来的频谱镜像问题
为了对连续信号做傅里叶变换,我们需要对信号进行采样,采样后得到的离散信号才可以用于计算机计算,做DFT。这里有一个采样导致的镜像问题。
首先,根据奈奎斯特采样定理:
要从抽样信号中无失真地恢复原信号,抽样频率应大于2倍信号最高频率。 抽样频率小于2倍频谱最高频率时,信号的频谱有混叠。 抽样频率大于2倍频谱最高频率时,信号的频谱无混叠。
说白了,要保留信号的基本信息,我们需要对信号进行信号至少两倍频率的采样。而数字设备采样可以看作连续信号乘以采样频率的狄拉克梳状函数。
这里需要注意一点,我刚刚的描述是连续信号乘以采样频率的狄拉克梳状函数,也就是说,采样实际上可以理解为被采样信号与采样信号相乘。根据卷积定理,信号时域相乘等于频域卷积。等于说被采样信号与采样信号做了混频。
假设被采样信号频率为100Hz,采样信号频率为1000Hz,那么对采样后的信号做DFT,在正频域上会得到100Hz,900Hz以及1100Hz的频谱。由于采样频率是1000Hz,因此在区间内会只有100Hz以及900Hz的频谱,这900Hz的频谱就是采样后离散信号的镜像。
奈奎斯特低通采样实际局限性
现如今通信设备采用的发送频率上到千兆,这对接收端ADC带来了很大的挑战。假设一个处于2GHz频段的信号,若要根据奈奎斯特(低通)采样率采样,则需要至少能做到4GHz的采样的ADC器件。先不说没有这么高频的采样芯片,就算有,成本也是巨大的。
再者,虽然信号处于2GHz的频段,但确实带通信号,只有处于2GHz周围的频段被用作数据传输,带传输带宽之外的频域没有信息传递。因此若对2GHz信号进行低通采样会造成极大的资源浪费。
但与单音信号不同的是,通信设备所发送的信号频率与带宽都是提前可知的,这对我们信号处理提供了有利条件。
带通采样
带通采样的原理可以理解为,利用采样函数对被采样函数做频谱搬移。注意,频谱搬移需要避免频率混叠,具体推导以及原理这篇博客做了详细叙述。
有点技术手段的可以参考这篇PDF
FFT诞生历史
1963年8月美、英、苏三国在莫斯科谈判,达成协议签定了该条约,全称为《关于禁止在大气层、外层空间和水下进行核武器爆炸实验的条约》又称〈部分核禁止条约〉或三家条约。可以注意到,条约中不包括地下核武器爆炸实验,这是因为地下核实验难以被检测到,大地隔绝了大部分的辐射,声音。使得其难以想地上或水下核试验一样容易被探测到。要想探测地下核试验,主要靠分析地动信息。但如何将日常地址活动造成的地动与核试验造成的地动区分开来成为了当时科学家所难以解决的问题。在快速傅里叶算法还未发现之前,按照离散傅里叶定义使用计算机对地动信号做频谱分析,算力远远不足,分析出的数据严重过时。因此在这个背景下,快速傅里叶变换的算法出现了。
快速傅里叶变换(FFT)
快速傅里叶算法本质上是对离散傅里叶变化的改进,本质上是利用矩阵乘法时不同基信号在奇数或偶数点的与被采样信号的乘积相同来减少计算,严格的数学推断可以参考这篇快速理解FFT算法(完整无废话)
MATLAB 仿真代码
1 | % 设置时间范围 |
